Question

I have a question on area of a triangle an area of a circle. See picture of my problem

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

equilateral triangle:

side = 7x

circle:

radius = 4r

Step 02:

area:

a = circle area - triangle area

triagle area:

triagle area = (b * h) / 2

b = 7x

h:

`\begin{gathered} (7x)^2=h^2+((7x)/(2))^2 \\ 49x^2=h^2+(49x^2)/(4) \\ h^2=49x^2-(49x^2)/(4)=(147x^2)/(4) \\ h\text{ = }\sqrt[]{(147x^2)/(4)\text{ }}=6.06x=6.1x \end{gathered}`

h = 6.1x

`\text{triangle area = }(7x\cdot6.1x)/(2)=(42.7x^2)/(2)=21.35x^2`

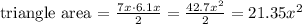
circle area:

circle area (r) = π r² = π (4r)² = 16 π r²

a = circle area - triangle area

a = 16 π r² - 21.35x²

The answer is:

a = 16 π r² - 21.35x²