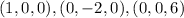SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given equation
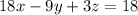
To get the intercepts, we pick a point and equate the others to zero and then solve for the point.
STEP 2: Get the values of x when y and z are zeroes
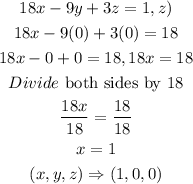
STEP 3: Get the values of y when x and z are zeroes
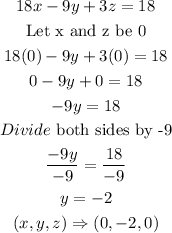
STEP 4: Get the value of z when x and y are zeroes
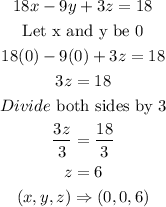
Hence, the intercepts are: