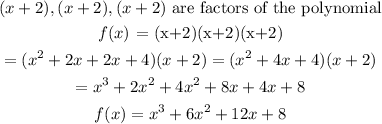Question

write a polynomial function in standard form with the given zeros. This is not a test nor homework, I am preparing for the ACT and my teacher said these problems would be on there and therefore I need help1. -1, 3, 42. -3, 0, 0, 53. -2 multiplicity 34. (x+3)^2(x+1)

Answer 1

For question 1

The zeros of the polynomial are -1, 3 , 4, it means x = -1, x=3 and x=4

therefore,

`\begin{gathered} x\text{ + 1, , x-3, and x-4 are factors of the polynomial} \\ \text{ f(x)= (x+1)(x-3)(x-4) } \\ f(x)=(x^2-3x+x-3)(x-4)^{} \\ =(x^2\text{ -2x -3)(x -4)} \\ =x^3-4x^2-2x^2+8x-3x+12 \\ f(x)=\text{ }x^3-6x^2+5x+12 \end{gathered}`

For question 2

The zeros of the polynomial are -3, 0, 0, 5 it means x = -3, x=0, x=0 and x=5

therefore,

`\begin{gathered} (x+3),\text{ (x-0), (x-0), and (x-5) are factors} \\ f(x)=\text{ (x+3) (x) (x) (x-5)} \\ =x^2(x+3)(x-5)=x^2(x^2-5x+3x-15)=x^2(x^2-2x-15) \\ f(x)=x^4-2x^3-15x^2 \end{gathered}`

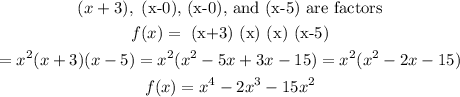
For question 3

The zeros of the polynomial are -2, -2, -2 it means x = -2, x=-2, , x=-2

therefore,

`\begin{gathered} (x+2),(x+2),(x+2)\text{ are factors of the polynomial} \\ f(x)\text{ = (x+2)(x+2)(x+2)} \\ =(x^2+2x+2x+4)(x+2)=(x^2+4x+4)(x+2) \\ =x^3+2x^2+4x^2+8x+4x+8 \\ f(x)=x^3+6x^2+12x+8 \end{gathered}`