We have two grading systems, with different weights for different items.
We have to calculate, for a certain points of the different items, which grading systems gives a higher weighted average score.
To do so we multiply each percentage to each of the items points and add them all.
We start with grading system 1:
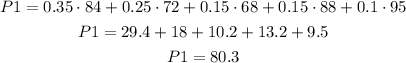
The grading system 1 gives an average score of 80.3.
We apply the grading system 2 coefficients and we get:
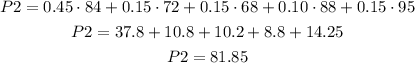
The grading system 2 gives an average score of 81.85.
With the grading system 2, the final score is a little higher than with grading system 1. So we would prefer the system 2.