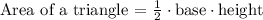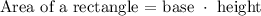Question

What is the surface area of the following solid? *13 ft 12ft 5ft 5ft

Answer 1

In order to calculate the total surface area we just need to sum the area of the different faces.

From the picture we see that we have the following faces.

- 2 x A (two triangles)

- S (a rectangle)

- T (a rectangle)

- B (the base rectangle)

Now me calculate the area of each one:

`A\text{ = }(1)/(2)\cdot12\cdot5\text{ = }30`

`S\text{ = 5}\cdot5=\text{ 25}`
`B=12\cdot5=60`
`T=13\cdot5=65`

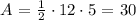
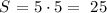
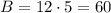
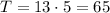
Now that we have the area of each face, we sum all the areas, taking in account the ones that appears twice:

`\text{Total area = 2}\cdot A+S+T+B=2\cdot30+25+60+65=210`

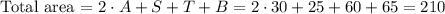
And, because the lenghts are measured in ft, the final answer is:

`\text{Total area = 210 ft}^2`

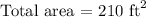
Note:

`\text{Area of a triangle = }(1)/(2)\cdot\text{base}\cdot\text{height}`
`\text{Area of a rectangle = base }\cdot\text{ height}`