1 Answer

Geinmachi · Answer 1 · 2023-12-10T14:11:28+0000

We can solve this by calculating the area of the square and subtracting the area of the inscribed circle. The area of the square is:

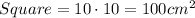
$Square=10\cdot10=100cm^2$

The formula for the area of a circle is:

$A=\pi r^2$

The radius of the inscribed circle is half the length of the side of the square, then, the radius is r = 5 cm

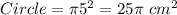
$Circle=\pi5^2=25\pi\text{ }cm^2$

Now, we rest:

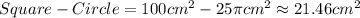
$Square-Circle=100cm^2-25\pi cm^2\approx21.46cm^2$

The answer is 21.46cm²

Please log in or register to add a comment.