Question

Make a question similar (but not the same!) to those in #2 Post your question and full solution

Answer 1

Write a function with vertical asymptote x=4, horizontal asymptote y=1, y intercept at (0,2).

A possible function can be express as:

`f(x)=(x-8)/(x-4)`

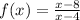
Let's prove that this function fulfils our conditions. Let's start with the y-intercept, we know that this happens when x=0, then we have:

`f(0)=(0-8)/(0-4)=2`

Hence the y-intercept is at (0,2).

Now, we know that a rational function has horizontal asymptote y=b if:

`\begin{gathered} \lim_(x\to\infty)f(x)=b \\ \text{ or } \\ \lim_(x\to-\infty)f(x)=b \end{gathered}`

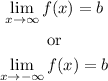
Let's find these limits:

`\begin{gathered} \lim_(x\to\infty)(x-8)/(x-4)=\lim_(x\to\infty)((x)/(x)-(8)/(x))/((x)/(x)-(4)/(x)) \\ =\lim_(x\to\infty)(1-(8)/(x))/(1-(4)/(x)) \\ =(1-0)/(1-0) \\ =1 \end{gathered}`

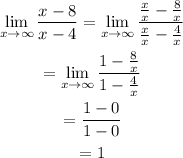
and:

`\begin{gathered} \lim_(x\to-\infty)(x-8)/(x-4)=\lim_(x\to-\infty)((x)/(x)-(8)/(x))/((x)/(x)-(4)/(x)) \\ =\lim_(x\to-\infty)(1-(8)/(x))/(1-(4)/(x)) \\ =(1-0)/(1-0) \\ =1 \end{gathered}`

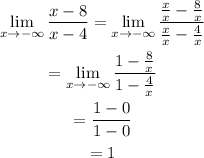
This means that we have a horizontal asymptote y=1 as we wanted.

Now, a rational function has vertical asymptote at x=a if:

`\begin{gathered} \lim_(x\to a^-)f(x)=\pm\infty \\ \text{ or } \\ \lim_(x\to a^+)f(x)=\pm\infty \end{gathered}`

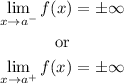
to determine the value of a we need to look where the function is not defined, that is, the values which make the denominator zero, in this case we have:

`\begin{gathered} x-4=0 \\ x=4 \end{gathered}`

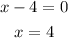
Then we need to find the limits:

`\begin{gathered} \lim_(x\to4^-)(x-8)/(x-4) \\ \text{ and } \\ \lim_(x\to4^+)(x-8)/(x-4) \end{gathered}`

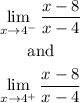
Now, if we approach the value x=4 from the left we notice that as x gets closer to 4 the function gets bigger and bigger, for example:

`f(3.9999)=(3.9999-8)/(3.9999-4)=400001`

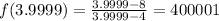
if we follow this procedure, we conclude that:

`\lim_(x\to4^-)(x-8)/(x-4)=\infty`

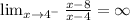
Similarly, if we approach x=4 from the right the function gets smaller and smaller, for example:

`f(4.0001)=(4.0001-8)/(4.0001-4)=-39999`

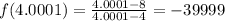
Then we can conclude that:

`\lim_(x\to4^+)(x-8)/(x-4)=-\infty`

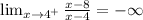
Hence, we conclude that the function we proposed has a vertical asymptote x=4 like we wanted.

the properties we gave can be seen in the following graph: