The first statement is about the diameter of the circle.
The diameter of a circle is always the double of its radius.
So if circle A ras a radius of 4 inches, its diameter is:
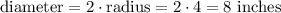
So the first statement is true (YES)
The second statement is about the area of the circle. The area of a circle is given by the following equation:
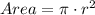
If the radius of the circle is 4 inches, we have:
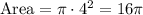
So the second statement is also true (YES)
The third statement is about the volume of a cylinder with a height of 6 inches and the circle A as the base. The volume of a cylinder is given by the equation:
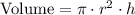
Using the radius = 4 inches and the height = 6 inches, we have:
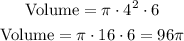
The volume is not 64pi, so this statement is false (NO).