Question

Savannah earned a score of 720 on Exam A that had a mean of 700 and a standarddeviation of 25. She is about to take Exam B that has a mean of 400 and a standarddeviation of 100. How well must Savannah score on Exam B in order to doequivalently well as she did on Exam A? Assume that scores on each exam arenormally distributed.

Answer 1

480

Step-by-step explanation:

First, we need to standardize the score on Exam A. It can standardize as

`z=\frac{\text{ score}-\text{ mean}}{\text{ standard deviation}}`

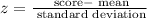
Replacing score = 720, mean = 700, and standard deviation = 25, we get

`z=(720-700)/(25)=(20)/(25)=0.8`

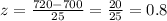
Then, to do equivalently well on exam B, we need a standard value equal to 0.8. So, the score can be calculated as

`\text{ score = z\lparen standard deviation\rparen + mean}`

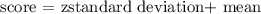
Replacing z = 0.8, standard deviation = 100 and mean = 400, we get

`\begin{gathered} \text{ score = 0.8\lparen100\rparen+400} \\ \text{ score = 80 + 400} \\ \text{ score = 480} \end{gathered}`

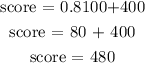
Therefore, the answer is 480