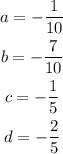We are given the following matrix:
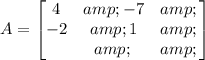
We are asked to determine the coefficients of:
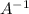
Which is the inverse matrix. To do that let's remember that the inverse of a 2 by 2 matrix of the form:
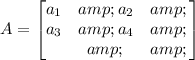
is:
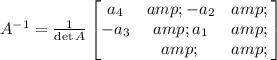
The value of the determinant of A (det A) is given by:
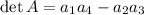
Replacing we get:

Replacing the values:
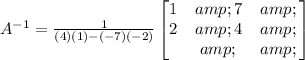
Solving the operations:
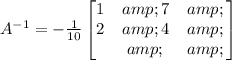
Or:
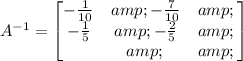
Therefore, we have: