Step 1- Write out the Future Value Ordinary Annuity formula:
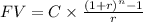
Where,

Step 2- Write out the given values and substitute them into the formula:
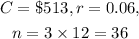
Substituting the given values into the formula, we have:
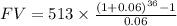
Hence,
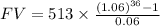
Hence, the future value is approximately:
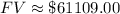
Hence, the amount in the account in 3 years is:
$61109.00