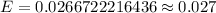We have here working with estimating a population proportion.
We have the following information from the question:
• The sample size, n, is equal to 1200 (n = 1200).
,
• We have that the fraction that responded "Yes" is 800.
,
• We need to find a 95% level of confidence for the margin error associated with the poll.
Now, we have the sample proportion for the sample size, n = 1200 is as follows:
Sample Proportion
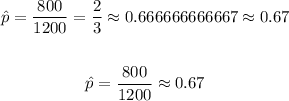
Therefore, the sample proportion for the sample size is 800/1200, which is, approximately, 0.67.
The margin of error associated with the poll
The margin of error, in this case, is given by the next formula:
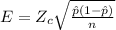
Where:

Now, we have that, for a level of confidence of 95%, the critical value is equal to z = 1.96:
Now, using all of the values at our disposal, we can use the formula to find the margin of error as follows:
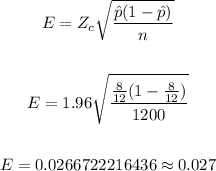
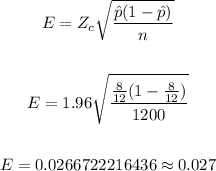
Therefore, in summary, we have that:
1. The sample proportion is:
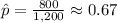
2. The margin of error associated with the poll is: