Question

I need help with this math question all parts pleasePart 2: find y-interceptPart 3: find the zerosPart 4: Graph k(x)

Answer 1

Given the following function:

`k(x)=x^3-5x^2`

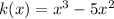
We will find the end behavior of the function.

the given function has a degree = 3 (odd)

And the leading coefficient is positive

the end behavior will be as follows:

`\begin{gathered} x\to-\infty\Rightarrow k(x)\to-\infty \\ x\to\infty\Rightarrow k(x)\to\infty \end{gathered}`

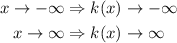
So, the answer will be:

The end behavior of the function is down to the left and up to the right.

===============================================================

Part (2), we will find the y-intercepts

The y-intercept is the value of y when x = 0

So, we will substitute x = 0 and then solve y

`y=0^3-5(0^2)=0`

So, the answer will be:

y-intercept = (0, 0)

================================================================

Part 3: we will find the zeros of k(x)

The zeros of the function are the values of x which make k(x) = 0

So, we will write the equation k(x) = 0 and then solve it for x.

`\begin{gathered} x^3-5x^2=0 \\ x^2(x-5)=0 \\ x^2=0\to x=0 \\ x-5=0\to x=5 \end{gathered}`

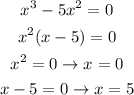
So, the answer will be:

Zeros of k: 0,5

===============================================================

Part 4: we will find the graph of k(x)

From the previous parts, we can conclude that

The graph of the function will be as shown in option D