Question

Solve the following equation y^4+7y^2-44=0

Answer 1

y = 2, y = -2, y = i √11, y = - i √ 11

Step-by-step explanation:

To solve the equation for y, we first make the substitution x = y^2. Doing this we write

`x^2+7x-44=0`

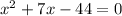
The above can be written as

`(x-4)(x+11)=0`

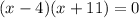
Which gives two equations

`\begin{gathered} x-4=0 \\ x+11=0 \end{gathered}`

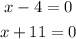
Substituting back x = y^2 gives

`\begin{gathered} y^2-4=0\rightarrow y=-2,y=2 \\ x^2+11=0\rightarrow y=i\sqrt[]{11},y=-i\sqrt[]{11} \end{gathered}`

Hence, to summarize, the solution to the equation is

`\begin{gathered} y=-2,y=2 \\ y=i\sqrt[]{11},y=-i\sqrt[]{11} \end{gathered}`