Question

Find the 12th term of the geometric sequence 1,3,9,...

Answer 1

find the 12th term of the geometric sequence 1,3,9,...​

we have

a1=1 ------> first term

a2=3

a3=9

Find the value of r (common ratio)

we have that

a2/a1=3/1=3

a3/a2=9/3=3

so

the common ratio is

r=3

we know that the general equation for a geometric sequence is

`a_n=a_1\cdot r^((n-1))`

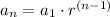
we have

a1=1

r=3

substitute

`\begin{gathered} a_n=1\cdot3^((n-1)) \\ a_n=3^((n-1)) \end{gathered}`

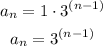
Find the 12th term

so

For n=12

substitute in the equation

`\begin{gathered} a_(12)=3^((12-1)) \\ a_(12)=3^((11)) \\ a_(12)=177,147 \end{gathered}`

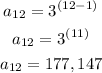
therefore

the answer is

177,147