A line equation can be written in slope-intercept form, which is

Where m represents the slope and b the y-intercept.
If we evaluate our points on this form, we're going to have a linear system where the solutions are those coefficients.
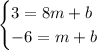
If we subtract the second equation from the first, we're going to have a new equation only for the slope.
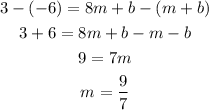
Now that we have the slope, we can use any of the equations to find the b value.
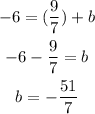
Then, our line equation is
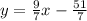
And this is the graph