Question

What does the constant 1.6 reveal about the rate of change of the quantity?

Answer 1

The form of the exponential growth/decay function is

`f(x)=a(1\pm r)^x`

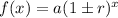
a is the initial amount

r is the rate of growth/decay per x years

We use + with growth and - with decay

Since the given function is

`f(t)=2700(1.6)^(7t)`

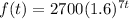
Where t is time per week

Compare the two functions

`\begin{gathered} a=2700 \\ (1+r)=1.6 \\ x=7t \end{gathered}`

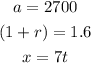
Since 1.6 is greater than 1, then

The function is growth

Equate 1.6 by (1 + r) to find r

`\begin{gathered} 1+r=1.6 \\ \\ 1-1+r=1.6-1 \\ \\ r=0.6 \end{gathered}`

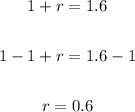
Change it to percent by multiplying it by 100%

`\begin{gathered} r=0.6*100\text{ \%} \\ \\ r=60\text{ \%} \end{gathered}`

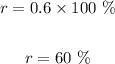
Since x = 7t then the time is every 7 weeks

The answer is

The function is growing exponentially at a rate of 60% every 7 weeks