Question

A standard deck of cards has 52 cards. Suppose you decide to play a game using only half of a standard deck. If you draw one card at a time from the half-deck, without replacement, how many different ways can you draw all of the cards? Remember that "without replacement" means that the cards are not returned to the deck after they are chosen. Write your answer in factorial notation.

Answer 1

We are asked to determine in how many ways we can draw all of the cards in half a deck. Since in a deck there are 52 cards, in half a deck there are:

`n=(52)/(2)=26`

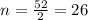
The number of ways in which the cards can be drawn is equivalent to the number of permutations. And this is equivalent to:

`P=n!`

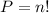
Where "p" is the number of permutations and n! is the factorial of the number of cards in half a deck. Substituting the values we get:

`P=26!`

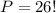
Solving the operations:

`P=403291461126605635584000000`

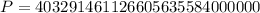
Thus we determine the number of ways the cards can be drawn.