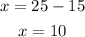To solve this problem we have to write an equation for each condition where the first charge is x and the second charge is y so:
For the total hours will be:
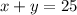
and the total charge will be:
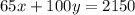
We can solve the first equation for x so:
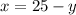
and we replace that in the secon equation so:
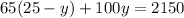
and we solve for y so:
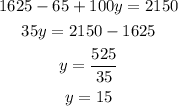
And with this value of y we can find x so: