Question

Hi can someone help me here​

Answer 1

`\left(x-(7)/(2)\right)^2+\left(y+(7)/(2)\right)^2=(25)/(2)`

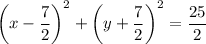
Explanation:

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

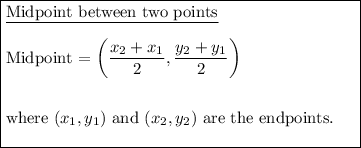
Given endpoints of the diameter of the circle:

• (x₁, y₁) = A (7, -3)
• (x₂, y₂) = B (0, -4)

To find the center of the circle, substitute the given endpoints into the midpoint formula:

`\begin{aligned} \implies \textsf{Midpoint} & =\left((0+7)/(2),(-4-3)/(2)\right)\\& =\left((7)/(2),-(7)/(2)\right)\end{aligned}`

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

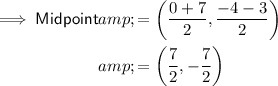
Substitute the found center and one of the given points (0, -4) into the equation and solve for r²:

`\implies \left(0-(7)/(2)\right)^2+\left(-4-\left(-(7)/(2)\right)\right)^2=r^2`

`\implies \left(-(7)/(2)\right)^2+\left(-(1)/(2)\right)^2=r^2`

`\implies (49)/(4)+(1)/(4)=r^2`

`\implies (50)/(4)=r^2`

`\implies r^2=(25)/(2)`

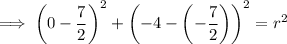
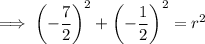
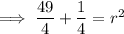
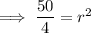
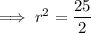
Therefore, the equation of the circle is:

`\implies \left(x-(7)/(2)\right)^2+\left(y+(7)/(2)\right)^2=(25)/(2)`

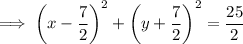
The graph of the circle is attached.