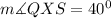Answer:
The value of angle QXS is;
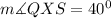
Step-by-step explanation:
From the given diagram in question 1:
We can see that angle QXT equals the sum of angle SXT and angle QXS;
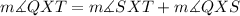
Given in the question is the value of angle SXT and angle QXS;
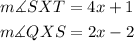
Substituting the values into the equation above;
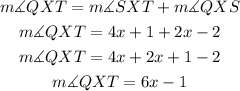
Since angle QXT is equal to 125 degree, then;
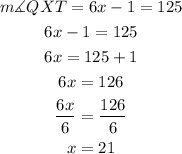
We can now substitute the value of x to get the value of angle QXS;
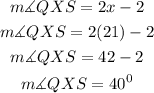
Therefore, the value of angle QXS is;