Question

f (x)=2^ x -10 and the domain of f(x) is the set of integers from 1 to 3which values are elements of the range of f(x) Select all that apply.a. -12b. -10c. -9d. -6e. -2

Answer 1

We have to find the range of the function f(x).

The definition of f(x) is:

`f(x)=2^x-10`

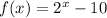
The domain of this function is defined as: D: {-1, 0, 1, 2, 3}, which represents all the integers from -1 to 3.

Then, we have to find the range by applying the function to each of the elements of the domain:

`f(-1)=2^(-1)-10=(1)/(2)-10=-9.5`
`f(0)=2^0-10=1-10=-9`
`f(1)=2^1-10=2-10=-8`
`f(2)=2^2-10=4-10=-6`
`f(3)=2^3-10=8-10=-2`

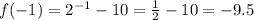
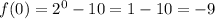
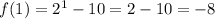
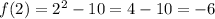
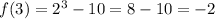
Then, the range of f(x) is R: {-9.5, -9, -8, -6, -2}.

Answer:

The options that apply from the list are -9, -6 and -2. [Options c, d and e]