Question

The diagonal of the figure Below represent the support beams for a patio covering.What IS the length of each support beam ? Given 30, and 10 yards

Answer 1

Since all the sides of the figure have the same length, then the figure is a rhombus. Then, its diagonals intersect at an angle of 90°.

Let O be the intersection of the diagonals of the rhombus. Notice that the triangle EOA is a right triangle. Since the side EA is the hypotenuse of the triangle, then, recalling the trigonometric functions:

`\begin{gathered} \cos (30)=(EO)/(EA) \\ \sin (30)=(OA)/(EA) \end{gathered}`

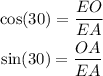
Use this information to solve for the segments EO and OA:

`\begin{gathered} EO=EA\cdot\cos (30) \\ =10\cdot\frac{\sqrt[]{3}}{2} \\ =5\cdot\sqrt[]{3} \end{gathered}`
`\begin{gathered} OA=EA\cdot\sin (30) \\ =10\cdot(1)/(2) \\ =5 \end{gathered}`

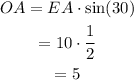
Since the diagonal EM is twice the segment EO and the diagonal BA is twice the segment OA, then the lengths of the diagonals are:

`\begin{gathered} BA=10 \\ EM=10\cdot\sqrt[]{3} \end{gathered}`

Therefore, the answer is:

`10\text{ yards and }10\cdot\sqrt[]{3}\text{ yards}`