Since all the sides of the figure have the same length, then the figure is a rhombus. Then, its diagonals intersect at an angle of 90°.
Let O be the intersection of the diagonals of the rhombus. Notice that the triangle EOA is a right triangle. Since the side EA is the hypotenuse of the triangle, then, recalling the trigonometric functions:
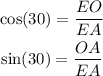
Use this information to solve for the segments EO and OA:
![\begin{gathered} EO=EA\cdot\cos (30) \\ =10\cdot\frac{\sqrt[]{3}}{2} \\ =5\cdot\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/e3iis5l21u2w1vrfayk89p726fzxonw6eo.png)
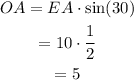
Since the diagonal EM is twice the segment EO and the diagonal BA is twice the segment OA, then the lengths of the diagonals are:
![\begin{gathered} BA=10 \\ EM=10\cdot\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/19lm8a1moq43hiun1mczq4qvhy5cfnk132.png)
Therefore, the answer is:
![10\text{ yards and }10\cdot\sqrt[]{3}\text{ yards}](https://img.qammunity.org/2023/formulas/mathematics/college/79wla2ys83b1n3nnm94wcn2qix3sredayi.png)