A right triangle is formed where the radius is one leg, the height is the other leg and the slant height is the hypotenuse. Applying the Pythagorean theorem:
![\begin{gathered} c^2=a^2+b^2 \\ s^2=27^2+36^2 \\ s^2=729+1296 \\ s^2=2025 \\ s=\sqrt[]{2025} \\ s=45\operatorname{cm} \end{gathered}]()
The surface area of a right cone is calculated as follows:
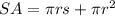
where r is the radius and s is the slant height. Substituting with r = 27 cm and s = 45 cm, we get:
![\begin{gathered} SA=\pi\cdot27\cdot45+\pi\cdot27^2 \\ SA=1215\pi+729\pi \\ SA=1215\pi+729\pi \\ SA=1944\pi\approx6107.25\operatorname{cm} \end{gathered}]()
The volume of a right cone is calculated as follows:
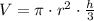
where h is the height. Substituting with r = 27 cm and h = 36 cm, we get:
![\begin{gathered} V=\pi\cdot27^2\cdot(36)/(3) \\ V=\pi\cdot729\cdot12 \\ V=8748\pi\approx27482.65\operatorname{cm}^3 \end{gathered}]()