Question

A couple took a small airplane for a flight to the wine country for a romantic dinner and then returned home. The plane flew a total of 5 hours and each way the trip was 233 miles. If the plane was flying at 170 miles per hour, what was the speed of the wind that affected the plane?

Answer 1

114.26 miles per hour

Explanation:

Let us call

v = wind speed

Then

speed with the wind = 170 + v

speed against the wind = 170 -v

Therefore,

The time taken on the outward journey ( with the wind):

`(233)/(170+v)`

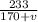
Time take on the return journey

`(233)/(170-v)`

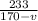
These two times must add up to 5 hours, the total time of the journey.

`(233)/(170+v)+(233)/(170-v)=5`

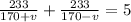
Solving the above equation for v will give us the wind speed.

The first step is to find the common denominator of the two rational expressions. We do this by multiplying the left rational expression by (180-v)/(180-v) and the right expression by (180 + v)/(180 + v).

`(170-v)/(170-v)*(233)/(170+v)+(233)/(170-v)*(170+v)/(170+v)=5`
`(233(170-v)+233(170+v))/((170-v)(170+v))=5`

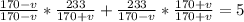
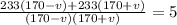
Dividing both sides by 233 gives

`((170-v)+(170+v))/((170-v)(170+v))=(5)/(233)`

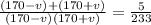
The numerator on the left-hand side of the equation simplifies to give

`(2*170)/((170-v)(170+v))=(5)/(233)`
`\Rightarrow(340)/((170-v)(170+v))=(5)/(233)`

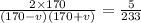
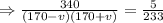
Expanding the denominator gives

`(340)/(28900-v^2)=(5)/(233)`

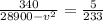
Cross multipication gives

`5(28900-v^2)=340*233`

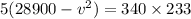
Dividing both sides by -5 gives

`v^2-28900=-(340*233)/(5)`
`v^2-28900=-15844`

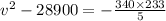
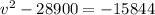
Adding 28900 to both sides gives

`v^2=13056`

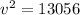
Finally, taking the sqaure root of both sides gives

`\boxed{v=114.26.}`

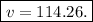
Hence, the speed of the wind, rounded to two decimal places, was 114.26 miles per hour.