Answer:
Question:
Determine whether each sequence is arithmetic. If so, identify the common difference. -34, -28, -22, -16
The numbers are given below as
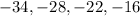
Concept:
Define an arithmetic sequence
An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.
The general form of an arithmetic sequence is given below as
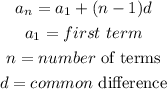
To check if they have a common difference, we will use the formulas below
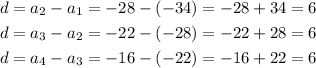
Hence,
Since the sequence has a common difference,
It is therefore an ARITHMETIC SEQUENCE
Their common difference is
