In a square, all the sides are the same length.
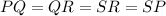
So, to find the length of the segment SR you can find the length of the segment QR using the formula of the distance between two points, that is:
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2^{}} \\ \text{ Where d is the distance between two points } \\ A(x_1,y_1)\text{ and} \\ B(x_2,y_2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8poid5el1ml6yzpluqtpbnvg0g5v725r85.png)
So, in this case, you have
![\begin{gathered} Q(7,0) \\ R(5,-8) \\ d=\sqrt[]{(5_{}-7)^2+(-8-0)^2} \\ d=\sqrt[]{(-2)^2+(-8)^2} \\ d=\sqrt[]{4+64} \\ d=\sqrt[]{68} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3px394nolwlhrapcphfefn4eq8n89bssv9.png)
Therefore, the length of the segment SR is
![\sqrt[]{68}](https://img.qammunity.org/2023/formulas/mathematics/college/wr916z4re21gy0bdy2v2uhcq2gmpc5k4ec.png)