Question

How many triangles exist that fit the following criteria?B = 30°, a = 4, b = 3

Answer 1

Given:

B = 30°, a = 4, b = 3

We will solve the triangle to find how many triangles exist that fit the given data

We will use the sine rule to find the angle A as follows:

`\begin{gathered} (a)/(sin(A))=(b)/(sin(B)) \\ \\ (4)/(sin(A))=(3)/(sin(30)) \\ \\ sin(A)=(4)/(3)sin(30)=(2)/(3) \\ \end{gathered}`

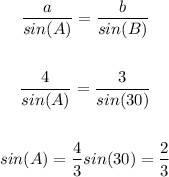
So, the measure of angle A will be as follows:

`A=sin^(-1)((2)/(3))=41.81\degree,or,138.19\degree`

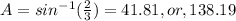
Now, we will find the measure of angle C using the fact that the sum of the angles = 180

So, there are two triangles that can fit the given data

So, the answer will be Two