Question

Two equally charged, 4.982 g spheres are placed with 3.173 cm between their centers. When released, each begins to accelerate at 258.312 m/s2. What is the magnitude of the charge, in micro-Coulombs, on each sphere?

Answer 1

Given:

The mass of the spheres is m = 4.982 g

The distance between the center of spheres is d = 3.173 cm

The acceleration is a = 258.312 m/s^2.

To find the magnitude of charge in micro Coulomb on each sphere.

Step-by-step explanation:

According to Newton's second law, the force will be

`F\text{ =ma}`

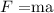
According to Coulomb's law, the force will be

`F=(kq^2)/(r^2)`

Here, k is the Coulomb's constant whose value is

`k=9*10^9\text{ N m}^2\text{ /C}^2`

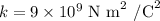
On equating the forces, the charge will be

`\begin{gathered} ma=(kq^2)/(r^2) \\ q=\sqrt{(mar^2)/(k)} \end{gathered}`

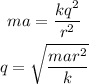
On substituting the values, the magnitude of charge will be

`\begin{gathered} q=\sqrt{((4.982*10^(-3))*258.312*(3.173*10^(-2))^2)/(9*10^9)} \\ =3.79\text{ }*10^(-7)\text{ C} \\ =0.379\text{ }*10^(-6)\text{ C} \\ =0.379\text{ }\mu C \end{gathered}`

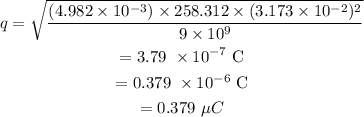
The magnitude of the charge of each sphere is 0.379 microCoulomb