Question

Is square root of 224 an irrational number ?

Answer 1

YES

Step-by-step explanation

We want to know if the square root of 224 is an irrational number.

An irrational number is a number that cannot be written as a fraction/ratio of two integers.

If we simplify the square root of 224:

`\begin{gathered} √(224)\text{ = }\sqrt{16\cdot\text{ 28}}\text{ = 4}√(28) \\ \text{ }\Rightarrow\text{ 21.166010488}\ldots \end{gathered}`

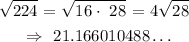
As we can see, this number cannot be written as a fraction of two numbers.

As a rule, the square root of any number that is not a perfect square is an irrational number.

So, the answer is Yes. It is an irrational number