SOLUTION:
Case: Local maxima and local minima
Given:
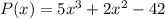
Required: To find the local maxima and minima
Method:
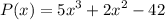
First the find the first derivative:
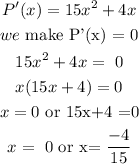
Let us take the points in the immediate neighbourhood of x = 0. The points are {-1, 1}.
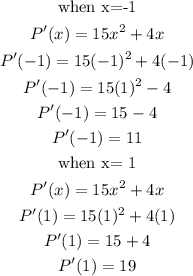
Let us take the points in the immediate neighbourhood of x = -4/15. The points are {-1, 0}
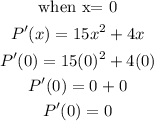
Final answer:
The local minima is at x= 0 while the local maxima is at x= -4/15