Answer:
∡BCA = 29
∡BOC = 58
Step-by-step explanation:
The angles BDC and BAC form the same arc on the circle, the arc BC. Then, these angles have the same measure, so
∡BCA = ∡BDC
∡BCA = 29
Then, we can use the inscribed angle theorem to find the arc BC as follows
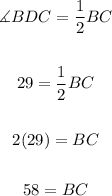
Therefore, arc BC has a measure of 58 degrees, which means that ∡BOC is equal to
∡BOC = Arc BC
∡BOC = 58
So, the answers are
∡BCA = 29
∡BOC = 58