Question

Use calculus to find the dimensions of a rectangle with area of 196 square-feet that has the smallest perimeter.

Answer 1

Step-by-step explanation

In the question, we are given that the area of the rectangle is;

`\text{Area}=196\text{ square fe}et`

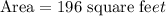
Recall that the area and perimeter of a rectangle are given by the formulas below.

`\begin{gathered} \text{Area = Lenth x Width = L}* W \\ \text{Perimeter = 2(L+W)} \end{gathered}`

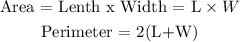
From the area of the rectangle, we can isolate the variable of the width.

`\begin{gathered} \text{Area}=\text{ L x W} \\ W=\frac{\text{Area}}{L} \\ W=(196)/(L) \end{gathered}`

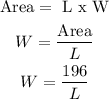
Therefore, the formula for the perimeter is transformed to give;

`\begin{gathered} \text{Perimeter = 2( L + }\frac{\text{196}}{L}) \\ \text{Simplifying the expression gives;} \\ P=2((L^2+196)/(L)) \\ P=\frac{2L^2+392^{}}{L} \\ P=2L+392L^(-1) \end{gathered}`

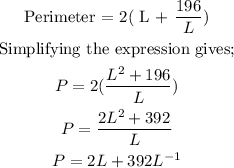
Recall, via the rules of differentiation

`\begin{gathered} \text{for y = x}^n \\ (dy)/(dx)=nx^(n-1) \end{gathered}`

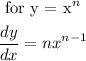
Therefore,

`\begin{gathered} (dP)/(dL)=2-392L^(-2)^{} \\ \text{But }(dP)/(dL)=0 \\ 0=2-392L^(-2) \\ 392^{}L^(-2)=2 \\ (1)/(L^2)=(2)/(392)^{} \\ L^2=(392)/(2) \\ L^2=196 \\ L=\sqrt[]{196} \\ L=14 \end{gathered}`

Since

`W=(196)/(L)=(196)/(14)=14`

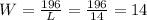
Answer: Length = 14 and Width = 14