For the given table representing the probability distribution, the probability of watching 2 movies is unknown.
The sum of all probabilities should be equal to 1. We can use that to calculate the unknown probability:
Adding all probabilities and equating to 1:
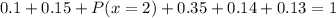
Solving for P(x=2)
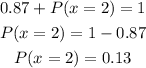
Then: A. The probability of watching 2 movies next month is 0.13.
The complete table of probability distribution will look like this:
xP(x)
00.1
10.15
20.13
30.35
40.14
50.13
To calculate the probability of watching more than two movies we need to add the probabilities of watching 3, 4 or 5 movies. Those should be added because those are the cases where more than 2 movies are watched.
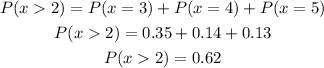
Then, B. The probability of watching more than 2 movies is 0.62.
The probability of watching 2 movies is equivalent to P(x>2) or P(x>=3).
On the other hand, to calculate P(X<4) or P(X<=3) we need to add the probabilities of watching 3 movies or less. That is, probabilities of watching 0, 1, 2 or 3:
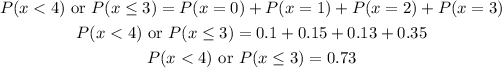
The probability of watching 3 movies or less next month is 0.73.
To estimate how much we would expect to spend per month if we pay for each movie sepparately we need to calculate the expected value of movies per month.
We can estimate that with the probability distribution given in the table.
The expected value is the sum of the products between each event and their probabilities:
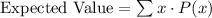
Let's call EV the expected value:
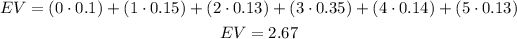
Then, we should expect to watch about 2.67 movies per month, on average.
I each individual movie costs $3.99, then, the total expenses per month will be:
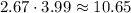
Then, C. According to the given probability distribution, we should expect to watch about 2.67 movies per month, on average, and spend in total $10.65 per month. We would be spending more than we would if we selected the unlimited movies plan which costs only $7.99 per month, then, it would be wise to decide to change our subscription to that plan.