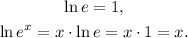1) We must solve for x the following equation:
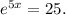
To solve this equation, we take the natural logarithm to both sides of the equation:
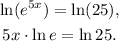
Now, we use the following results:
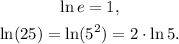
Replacing these results in the equation above, we have:
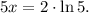
Solving for x, we get:
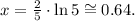
2) We must solve for x the following equation:
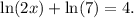
To solve this problem, we isolate the part that involves the x:
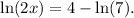
Now, using the following property:
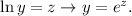
with:
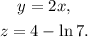
we have:
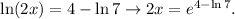
Solving the last equation for x, we get:
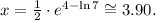
Answers
1) The value of x that solves the first equation is 0.64 to two decimal places.
2) The value of x that solves the second equation is 3.90 to two decimal places.
Review of the base of a logarithm
We can define the logarithm in base a through the following equations:
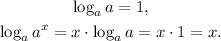
When we use as a base the Euler number e ≅ 2.718, the logarithm is called "natural" and we use the following notation for it:
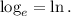
With this notation, we have the following properties: