Question

accounts that earn 6% interest. If Emma’saccount earns simple interest and Paul’saccount earns compound interest, which is thevalue of each person’s account after 8 years?A. Emma – $2,960; Paul – $3,187.708. Emma – $960; Paul – $3,187.70C. Emma – $2,960; Paut- $ 1,187.70

Answer 1

So,

Remember that the simple interest of an initial amount after "t" years, can be found using the following formula:

`A=P(1+rt)`

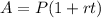
Where A is the final amount, P is the initial amount, r is the rate and t are the years involved.

If we replace our values, Emma will has the following amount after 8 years:

`\begin{gathered} A=2000(1+(6)/(100)(8)) \\ A=2960 \end{gathered}`

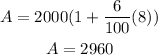
So, Emma will has $2,960 after 8 years.

To find the amount that Paul will has, we should remember what the compound interest is.

Remember that the compound interest is given by the formula:

`A=P(1+i)^n`

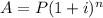
Where A is the final amount, P is the initial amount, i is the rate and n are the years involved.

If we replace our values, Paul will has the following amount of money after 8 years:

`\begin{gathered} A=2000(1+(6)/(100))^8 \\ A=3187.70 \end{gathered}`

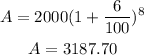
So, Paul will has $3187,70 after 8 years.

Therefore, the correct answer is A.