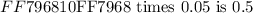We will look at the process of decimal point shifts as follows:
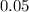
For the above decimal to be manipulated in such a way such that the result is:
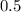
Here we see that the digits in the given decimal and the result are exactly the same. However, the placement of decimal point ( . ) has been changed. Such changes in decimal point places are usually accompained by number multiples of ( 10 ).
Now there are two possibilities for the decimal point to move i.e to the right or to the left. If we move the decimal point to the left then we are reducing the value of the decimal ( smaller number ). In such cases we divide the given decimal by multiples of ( 10 ).
Vice versa, If we move the decimal point to the right then we are increasing the value of the decimal ( larger number ). In such cases we multiply the given decimal by multiples of ( 10 ).
The decimal number given to us is smaller than the result decimal. i.e:
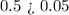
Hence, the given decimal number must be multipled by multiples of 10.
The general rule in moving the decimal point in either multiplying or dividing the multiples of ( 10 )s. Is to count the number of " 0 s" in the this multiples. E.g if we divide:
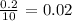
In above example we divided by ( 10 ). This has ( one zero ). Hence, we will move the decimal point to the left by ( one place ). Another example:
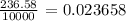
In above example we divided by ( 10000 ). This has ( four zeros ). Hence, we will move the decimal point to the left by ( four places ).
The same case applies to multiplication of multiples of 10; however, the only difference is the direction of decimal point moving i.e right.
So with the help of above guidelines and example we see that:
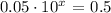
We need to determine the number of zeroes for ( 10s ) for which there is only a one place shift to the right side by the decimal point.
The value must be ( x = 1 ). That is we multiple the given ( 0.05 ) by ( 10 ). 10 has only one zero which allow the decimal point to travel to the right side by one digit place. Hence,
Answer: