Question

The perimeter of rectangle A is 10 cm and its area is 6 cm2. The perimeter of rectangle B is 20 cm. What is the area of rectangle B assuming these two rectangles are similar?

Answer 1

The perimeter of rectangle A is 10 cm

Perimeter of A = 2x+2y=10 cm, then:

Perimeter of A = 2(x+y)=10

Perimeter of A = x+y=5

We also know that the area of A= xy= 6 cm²

Then, we can admit x=3 and y=2.

Both rectangles are similar.

`\frac{x_a}{y_a_{}}=(x_b)/(y_b)`

`\begin{gathered} (3)/(2)=(x_b)/(y_b) \\ x_b=\frac{3y_b}{2_{}} \end{gathered}`

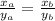
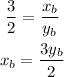
Perimeter of B

`\begin{gathered} 2x_b+2y_b=20 \\ x_b+y_b=10 \\ (3y_b)/(2)+y_b=10 \\ 3y_b+2y_b=20 \\ 5y_b=20 \\ y_b=4 \end{gathered}`
`\begin{gathered} x_b=(3y_b)/(2) \\ x_b=(3\cdot4)/(2) \\ x_b=(12)/(2) \\ x_b=6 \end{gathered}`

Therefore

Area of B = 4 x 6 cm² = 24 cm²