Question

I have started number 7 but am not so sure about my answer just wanted to see if I was doing the problem right way.

Answer 1

To get a probability in a given set, we need to count the events we want to happen and divide by the total possibilities.

a) Here, we have a set that goes from 1 to 12, so there is 12 possibilities. We want to pick a prime number, so we need to count how many primes we have in this set.

1 is not prime.

Also, 4, 6, 8, 9, 10 and 12 are not primes.

So, we have the primes: 2, 3, 5, 7 and 11. There are 5.

So, the probability will be:

`P=(5)/(12)\approx0.42`

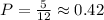
b) Assuming the die are 6-sided going from 1 to 6, we can obtain the numbers from 1 + 1 = 2 until 6 + 6 = 12. However, there are differento number of possibilities. We still are looking for 2, 3, 5, 7 and 11, however now we have a total of 6 times 6 possibilities:

`C_T=6\cdot6=36`

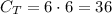
And we have to calculate the combinations for each prime and add them.

2: there is only 1 + 1, so:

`C_2=1`

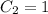
3: We can do 1 + 2 and 2 + 1, so there are 2:

`C_3=2`

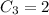
5: We have 1 + 4, 2 + 3, 3 + 2 and 4 + 1, so 4 possibilities:

`C_5=4`

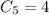
7: We have 1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2 and 6 + 1, 6 possibilities:

`C_7=6`

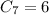
11: We have 5 + 6 and 6 + 5 only. 2 possitilities:

`C_(11)=2`

In total, we have:

`C_2+C_3+C_5+C_7+C_(11)=1+2+4+6+2=15_{}`

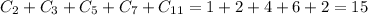
So, the probability will be:

`P=(15)/(36)\approx0.42`

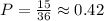
It ended up being the same.