The numerator of the left hand side can be rewritten as:
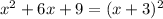
Then, the given equation can be written as:
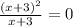
Since
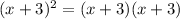
we have
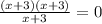
We can to can cancel out one term x+3 and get
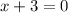
which gives

Finally, in order to check that this value corresponds to a real answer, we need to subsitute this value into the equation and compute the limit when x approaches to -3, that is,
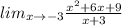
which gives
![l\imaginaryI m_{x\operatorname{\rightarrow}-3}(x^(2)+6x+9)/(x+3)=(0)/(0)]()
Since the limit has the form 0/0 we can to apply L'Hopital rule, that is,
![l\imaginaryI m_{x\operatorname{\rightarrow}-3}((d)/(dx)(x^2+6x+9))/((d)/(dx)(x+3))]()
which gives
![l\imaginaryI m_{x\operatorname{\rightarrow}-3}((d)/(dx)(x^(2)+6x+9))/((d)/(dx)(x+3))=l\imaginaryI m_{x\operatorname{\rightarrow}-3}(2x+6)/(1)=(0)/(1)=0]()
Since the limit exists and is equal to zero then the solution of the equation is: x= -3