Question

Stats To quality for a police academy, applicants are given a lest of physical Itness. Ihe scores are normallyDistributed with a mean of 64 and a standard deviation of 9. If only the top 20% of the applicants are selected,Find the cutoff score.

Answer 1

Since we want just the top 20% applicants and the data is normally distributed, we can use a z-score table to check the z-score that gives this percentage.

The z-score table usually shows the percentage for the values below a certain z-score, but since the whole distribution accounts to 100%, we can do the following.

We want a z* such that:

`P(z>z^*)=0.20`

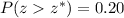
But, to use a value that is in a z-score table, we do the following:

`\begin{gathered} P(zz^*)=1 \\ P(zz^*)=1-0.20=0.80 \end{gathered}`

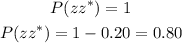
So, we want a z-score that give a percentage of 80% for the value below it.

Using the z-score table or a z-score calculator, we can see that:

Where z is the z-score we have, μ is the mean and σ is the standard deviation, so:

`\begin{gathered} x=0.8416\cdot9+64 \\ x=7.5744.64 \\ x=71.5744\cong72 \end{gathered}`

so, the cutoff score is approximately 72.