Question

In ΔKLM, the measure of ∠M =90°, the measure of ∠K=,86°, and MK = 86 feet. Find the length of KL to the nearest tenth of a foot.

Answer 1

ΔKLM is a right triangle, the following measures are known:

∠M= 90º

∠K=86º

MK= 86 feet

The side KL is the hypotenuse of the right triangle. To determine its measure you have to apply the trigonometric ratios. In this case, we know one of the angles of the triangle and the length of the side next to the angle, the trigonometric ratio that relates the adjacent side and the hypotenuse is the cosine:

`\cos \theta=(adjacent)/(hypotenuse)`

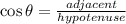
From this expression, you can calculate the measure of the hypotenuse.

`\cos 86=(86)/(x)`

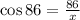
-Multiply both sides of the expression by x to take the term out of the denominators place:

`\begin{gathered} x\cos 86=x\cdot(86)/(x) \\ x\cos 86=86 \end{gathered}`

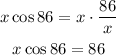
-Divide both sides of the expression by cos 86 to reach the value of x:

`\begin{gathered} x\cdot(\cos86)/(\cos86)=(86)/(\cos 86) \\ x=(86)/(\cos 86) \\ x=1232.86 \\ x\approx1232.9ft \end{gathered}`

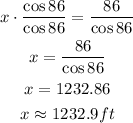
The length of KL is equal to 1232.9ft