Let 'y' represent the amount Margaret spent at the state fair.
Let 'x' represent the amount Nathan spent at the state fair.
In the next statement, Nathan spent $2 more than twice the amount that Margaret spent.
Mathematically,
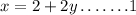
And also, we were told that Margaret and Nathan spent a total of $128 at the state fair.
Mathematically,
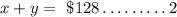
Let us substitute 'x'= 2+2y into equation 2 and solve for y.
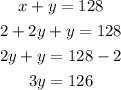
Divide both sides by 3
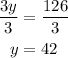
Therefore, the amount of money spent by Nathan will be,
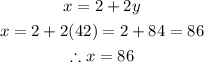
Hence, Nathan spent $86 at the fair.