Question

A shop sign weighing 215 N hangs from the end of auniform 175-N beam as shown in (Figure 1).Find the tension in the supporting wire (at 35.0 degrees)

Answer 1

Decomposing the tension into vertical and horizontal components, and considering vertical force equilibrium, the tension in the supporting wire is approximately 679.94 N, maintaining stability in the system with a hanging sign weighing 215 N on a 175 N beam.

1. Decompose Tension into Components:

`\( T_x = T \cdot \cos(35^\circ) \)\\ \( T_y = T \cdot \sin(35^\circ) \)`

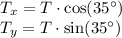
2. Vertical Force Equilibrium:

`\( T_y - 175 \, \text{N} - 215 \, \text{N} = 0 \)\\ \( T_y - 390 \, \text{N} = 0 \)\\ \( T_y = 390 \, \text{N} \)`

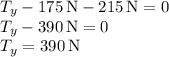
3. Tension in the Wire:

`\( T \cdot \sin(35^\circ) = 390 \, \text{N} \)\\ \( T \cdot 0.57358 = 390 \, \text{N} \)\\ \( T = \frac{390 \, \text{N}}{0.57358} \)\\ \( T \approx 679.94 \, \text{N} \)`

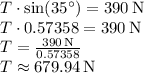
Therefore, the tension in the supporting wire is approximately
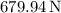`\( 679.94 \, \text{N} \)`.

Answer 2

In order to find the tension in the wire, let's first decompose it in its vertical and horizontal components:

`\begin{gathered} T_x=T\cdot\cos (35\degree) \\ T_y=T\cdot\sin (35\degree) \end{gathered}`

Now, since the system is stable, the sum of vertical forces is equal to zero, so we have:

`\begin{gathered} T_y-175-215=0 \\ T_y-390=0 \\ T_y=390 \\ T\cdot\sin (35\degree)=390 \\ T\cdot0.57358=390 \\ T=(390)/(0.57358) \\ T=679.94\text{ N} \end{gathered}`

So the tension in the wire is equal to 679.94 N.