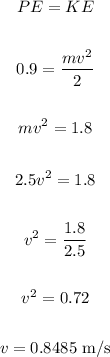Question

In FIGURE 2, a block of mass m=2.5 kg slides heads on into a spring of spring constant k=320 N/m. When the block stops, it has compressed the spring by 7.5 cm. The coefficient of kinetic friction between block and floor is 0.25. While the block is in contact with the spring and being brought to rest, calculatea. the work done by the spring force.b. the increase in thermal energy of the block-floor system.c. What is the block's speed just as it reaches the spring?

Answer 1

(a)

The work done by the spring force can be calculated with the formula below:

`W=(1)/(2)kx^2`

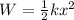
Using k = 320 N/m and x = 0.075 m, we have:

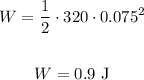
`\begin{gathered} W=(1)/(2)\cdot320\cdot0.075^2\\ \\ W=0.9\text{ J} \end{gathered}`

(b)

The increase in thermal energy is given by the work done by the friction force.

To calculate this work, first let's find the friction force:

`\begin{gathered} F_(friction)=F_(normal)\cdot\mu\\ \\ F_(friction)=m\cdot g\cdot\mu\\ \\ F_(friction)=2.5\cdot9.8\cdot0.25\\ \\ F_(friction)=6.125\text{ N} \end{gathered}`

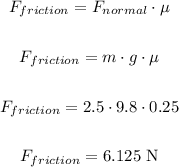
Now, calculating the work, we have:

`\begin{gathered} W=F\cdot d\\ \\ W=6.125\cdot0.075\\ \\ W=0.46\text{ J} \end{gathered}`

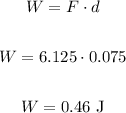
(c)

The block speed can be found by converting the potential energy from the spring (same value of the calculated work in item a) into kinetic energy for the block:

`\begin{gathered} PE=KE\\ \\ 0.9=(mv^2)/(2)\\ \\ mv^2=1.8\\ \\ 2.5v^2=1.8\\ \\ v^2=(1.8)/(2.5)\\ \\ v^2=0.72\\ \\ v=0.8485\text{ m/s} \end{gathered}`