Question

Find the measure of indicated angle. Round to the 10th.

Answer 1

29.6 °

Step-by-step explanation

we have a right triangle( a triangle with an angle of 90°), so we can use a trigonometric function

so

Step 1

a) Let

`\begin{gathered} \text{angle}=\text{ ?} \\ \text{ hypotenuse( the longest side)= 23} \\ adjacent\text{ side= }20 \end{gathered}`

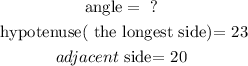
so, we need to use a function that relates those values, it is

`\begin{gathered} \cos \emptyset=\frac{adjacen\text{t side}}{\text{hypotenuse }} \\ \text{where }\emptyset\text{ is the angle} \end{gathered}`

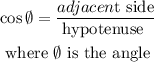
b) replace the values in the function and solve for the angle

`\begin{gathered} \cos \emptyset=\frac{adjacen\text{t side}}{\text{hypotenuse }} \\ \cos \text{ ? =}(20)/(23) \\ \text{ inverse cosine in both sides } \\ \cos ^(-1)(^{}\cos \text{ ?) =}\cos ^(-1)((20)/(23)) \\ \text{ ? = }29.59\text{ \degree} \\ \text{rounded to 10th} \\ \text{ ? = }29.6\text{ \degree} \end{gathered}`

therefore, the answer is

29.6

I hope this helps you