Question

What is 3[cos(60)+isin60]*1/2[cos(15)+isin(15)]

Answer 1

`\frac{3\left(-1\right)^{(5)/(12)}}{2}`

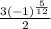
1) Let's simplify this expression considering the trigonometric ratios and the complex numbers as well.

`\begin{gathered} 3\left[\cos \left(60^(\circ \:)\right)+i\sin \left(60^(\circ \:)\right)\right](1)/(2)\left[\cos \left(15^(\circ \:)\right)+i\sin \left(15^(\circ \:)\right)\right] \\ Convert\:to\:radians: \\ 3\left[\cos \left((\pi )/(3)\right)+i\sin \left((\pi )/(3)\right)\right](1)/(2)\left[\cos \left((\pi )/(12)\right)+i\sin \left((\pi )/(12)\right)\right] \\ \quad \cos \left(x\right)+i\sin \left(x\right)=e^(ix) \\ 3*(1)/(2)\lbrack\left[e^{i(\pi)/(3)}\right]\left[e^{i(\pi)/(12)}\right] \\ \frac{3\left(-1\right)^{(5)/(12)}}{2} \\ \end{gathered}`

We have transitioned that to work with radians for convenience and used one identity. Note that we could have written our final answer in a radical form.