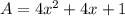Question

The length of a side of a square is (2x + 1) km. Find the area of thesquare in terms of the variable x

Answer 1

The area of the square is given by:

`A=s^2`

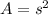
Where s is the length of the side. Then s=(2x+1) km.

By replacing this into the formula we have:

`A=(2x+1)^2`

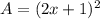
Also, the square of a sum is given by:

`(a+b)^2=a^2+2ab+b^2`

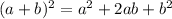
If a=2x and b=1, then:

`\begin{gathered} (2x+1)^2=(2x)^2+2(2x)(1)+(1)^2 \\ (2x+1)^2=4x^2+4x+1 \end{gathered}`

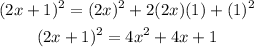
Thus, the area of the square in terms of the variable x is:

`A=4x^2+4x+1`