Question

how do I solve for x intercepts of this equation. I'm having trouble solving it.
`y = 2x ^(2) + 12x + 13`

Answer 1

`y=2x^2+12x+13`

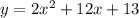
To find the x-intercepts of this equation, substitute y by 0 at first

`0=2x^2+12x+13`

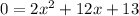
Now we need to factor this equation into 2 factors

We need 2 numbers their sum = 12 (the middle term)

But we can not find them mentally, then we will use the formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

a is the coefficient of x^2

b is the coefficient of x

c is the numerical term

a = 2, b = 12, c = 13

Let us substitute them in the rule to find x

`\begin{gathered} x=\frac{-12+\sqrt[]{(12)^2-4(2)(13)}}{2(2)} \\ x=\frac{-12+\sqrt[]{144-104}}{4} \\ x=\frac{-12+\sqrt[]{40}}{4} \end{gathered}`

We will simplify the root

`x=\frac{-12+2\sqrt[]{10}}{4}`

Divide up and down by 2 to simplify the fraction

`x=\frac{-6+\sqrt[]{10}}{2}`

The 2nd root will be the same number but a different middle sign

`x=\frac{-6-\sqrt[]{10}}{2}`

The x-intercepts are

`(\frac{-6+\sqrt[]{10}}{2},0)\text{and(}\frac{-6-\sqrt[]{10}}{2},0)`